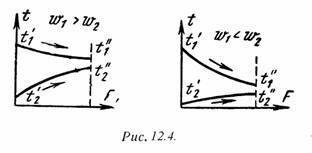
Принцип расчета теплового потока через цилиндрическую стенку аналогична как и для плоской стенки. Рассмотрим однородную трубу (рис.12.2) с теплопроводностью l, внутренний диаметр d1, наружный диаметр d2, длина l. Внутри трубы находится горячая среда с температурой t\’ж, а снаружи холодная среда с температурой t\’\’ж.
Тепловой поток, переданный от горячей среды к внутренней стенке трубы по закону Ньютона-Рихмана имеет вид:
Q = p·d1·a1·l·(t\’ж – t1) , (12.9)
где a1 – коэффициент теплоотдачи от горячей среды с температурой t\’ж к поверхности стенки с температурой t1;
Тепловой поток, переданный через стенку трубы, определяется по уравнению:
Q = 2·p·l·l·(t1 – t2) / ln (d2/d1). (12.10)
Тепловой поток от второй поверхности стенки трубы к холодной среде определяется по формуле:
Q = p·d2·a2·l·(t1 — t\’\’ж) , (12.11)
где a2 – коэффициент теплоотдачи от второй поверхности стенки к холодной среде с температурой t\’\’ж.
Решая эти три уравнения получаем:
Q = p l·(t\’ж – t\’\’ж) • К, (12.12)
где Кl = 1/[1/(a1d1) + 1/(2lln(d2/d1) + 1/(a2d2)] (12.13)
— линейный коэффициент теплопередачи,
или Rl = 1/ Кl = [1/(a1d1) + 1/(2lln(d2/d1) + 1/(a2d2)] (12.14)
— полное линейное термическое сопротивление
теплопередачи через однослойную цилиндрическую стенку.
1/(a1d1), 1/(a2d2) – термические сопротивления теплоотдачи поверхностей стенки;
1/(2lln(d2/d1) — термическое сопротивление стенки.
Для многослойной (n слоев) цилиндрической стенки полное линейное термическое сопротивление будет определяться по следующей формуле:
Rl = 1/ Кl = [1/(a1d1) + 1/(2l1ln(d2/d1) + 1/(2l3ln(d3/d2) + …
+ 1/(2lnln(dn+1/dn) + 1/(a2dn)] (12.15)